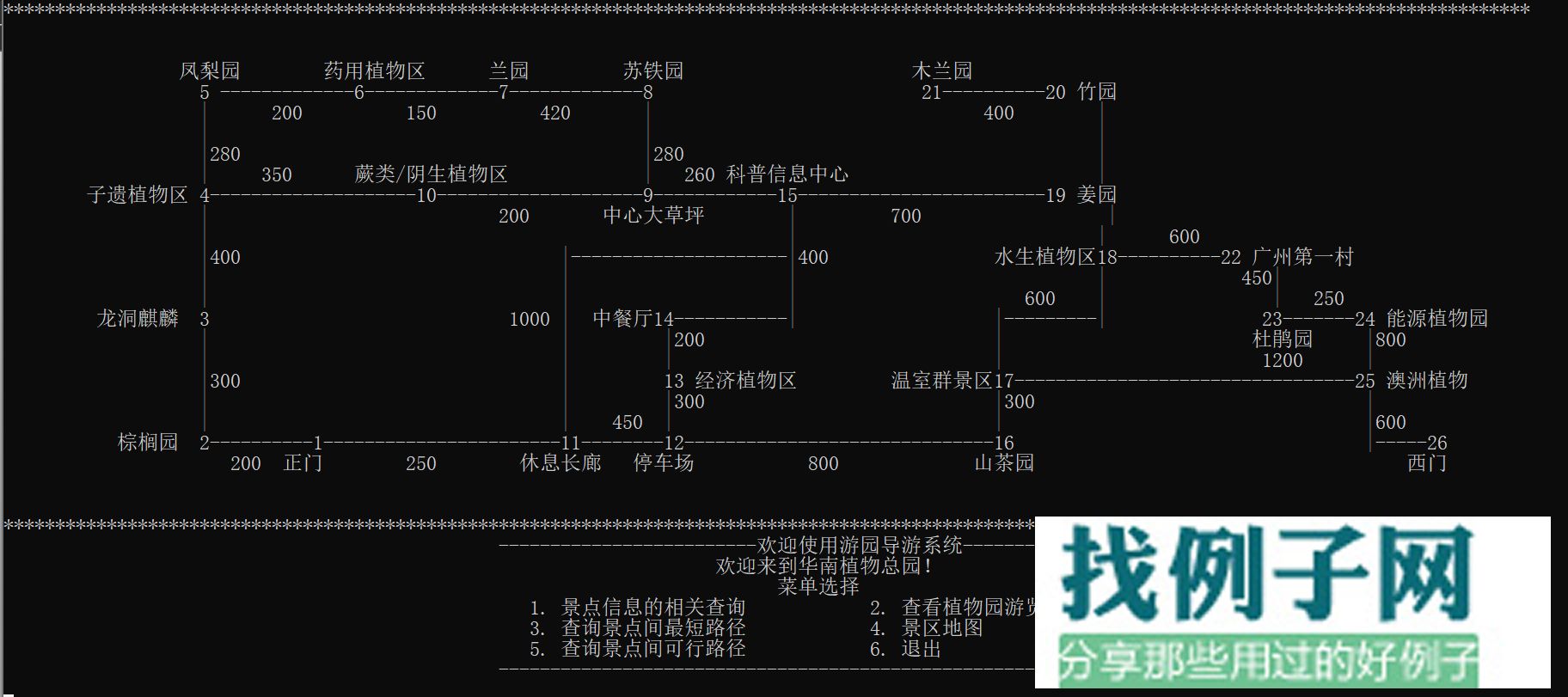
景区园区导航图代码.cpp 在旅游景区,经常会遇到游客打听从一个景点到另一个景点的最短路径和最短距离,这类游客不喜欢按照导游图的线路来游览,而是挑选自己感兴趣的景点游览。为于帮助这类游客信息查询,就需要计算出所有景点之间最短路径和最短距离。算法采用弗洛伊德算法均可。建立一个景区旅游信息管理系统,实现的主要功能包括制订旅游景点导游线路策略和制订景区道路铺设策略。本例以华南植物园景点为例进行设计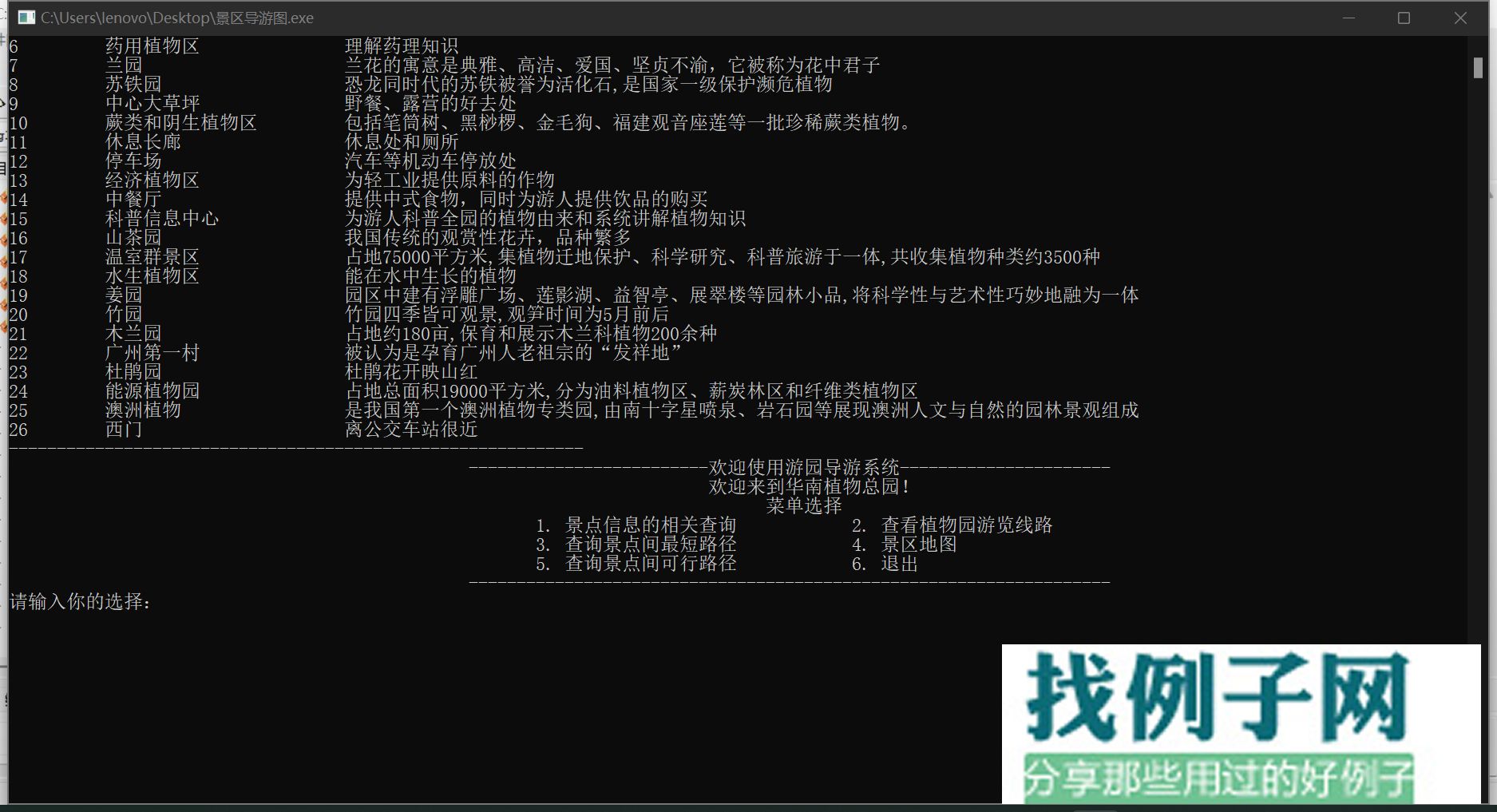
//输出序号为(m,n)景点间的长度,不超过8个景点的路径
void path(mgraph c,int n,int k)
{ //递归调用函数。若顶点s是由m出发到景点n的路径上的顶点,则调用自身,求由s出发的所有可能到达
//顶点n的路径。找到一条(递归出口),输出一条(限制只输出景点个数≤的路径)。
//d[]数组存储由m出发到景点n的路径上的顶点编号,visited[]数组用于存放顶点是否被访问的标志。
int s,x=0,t=k 1; //t用于存放路径上下一个顶点对应的d[]数组元素的下标
if(d[k]==n && k<15) //若d[k]是终点n且景点个数≤8,则输出该路径
{
for(s=0;s<k;s )
printf("%s--->",c.vexs[d[s]].name); //输出该路径。s=0时为起点m
printf("%s\n\n",c.vexs[d[s]].name); //输出最后一个景点名(顶点n的名字,此时s==k)
}
else
{
s=0;
while(s<c.vexnum) //从第m个顶点,试探至所有顶点是否有路径
{
if((c.arcs[d[k]][s].adj<Infinity)&&(visited[s]==0))
//初态:顶点m到顶点s有边且末被 访问
{
visited[s]=1;
d[k 1]=s; //存储顶点s至d[k 1]
path(c,n,t); //求从下标为t=k 1的第d[t]==s个顶点开始的路径
//(递归调用),同时输出一条m至n的路径
visited[s]=0; //将捞到的路径上顶点的访问标志重新设置为0,以用于试探新的路径
}
s ; //试探从下一个顶点s开始是否有到绺的路径
}//endwhile
}//endelse
}//endpath



评论